Postulados De Golomb Para Secuencias Cifrantes
Son herramienta que ayudan a determinar la calidad y
seguridad de una secuencia en términos de aleatoriedad (primero y seguno
postulados) y su impredecibilidad(tercer postulador).
Una pequeña definición
En 1967 Golomb, formulo tres postulados que en una
secuencia finita debe satisfacer para denominarse secuencia pseudoaleatoria o
PN (Pseudo Noise). Estos postulados pueden resumirse de la siguiente manera, en
cada periodo de la secuencia considerada:
G1: El número de 1 tiene que ser aproximadamente igual al número de
0. Es decir, el número de 1 en cada periodo debe diferir del número de 0 por no
más que 1.
G2: La probabilidad de ocurrencia, aproximada por su
frecuencia relativa, de cada k-grama (muestras de n dígitos consecutivos) debe
ser muy cercana a :
G3: La función de auto correlación, AC(K), fuera de fase es
constante para todo valor de K. Para que una secuencia satisfaga este
postulado, la función de auto correlación debe ser bivaluada. Una secuencia que cumpla estos tres postulados se denomina
secuencia pseudoaleatoria, PN y disfruta de todas las propiedades de una
secuencia binaria con distribución uniforme.
INTERPRETACIÓN DE LOS POSTULADOS DE GOLOMB G1 Y G2
Debido a la importancia de aplicación de los postulados, a
continuación se dará una interpretación y se mostrará como es que el postulado
G2 de Golomb implica de manera directa con la prueba de aleatoriedad que sugiere
M.J.B Robshaw de RSA Laboratories, en la que se involucra una comparación de la
secuencia pseudoaleatoria generada contra una secuencia verdaderamente
aleatoria.
INTERPRETACIÓN DE G1
La interpretación de este postulado establece que los dos
símbolos usados, en este caso 0 y 1 deben aparecer con la misma probabilidad en
la secuencia generada. A pesar de que en el análisis de una secuencia se cumpla
este postulado, no existe ninguna garantía de que la secuencia analizada posea
una distribución uniforme, por lo que, se requiere analizar la constitución de
la secuencia considerando la ocurrencia de n-gramas, tal y como lo establece
implícitamente el postulado G2.
INTERPRETACIÓN DE G2
El propósito de este postulado es verificar que el número de
ocurrencias de la n-grama es aproximadamente el mismo, como cabría de esperarse
en una secuencia aleatoria. Una grama de longitud n es una subsecuencia tomada
a partir de una posición arbitraria de la secuencia pseudoaleatoria. En
general, existen 2k n-gramas de longitud
k. En una secuencia de longitud K, para K=1, 2, 3,… se tiene:
De lo cual se puede observar que la probabilidad de
ocurrencia de cada k-grama es:
Donde, Na es el número de veces que ocurre las combinaciones
de las diferentes gramas, y K-n es el número total de veces que ocurre los
k-gramas. Para analizar una secuencia binaria pseudoaleatoria con una
longitud K dígitos, primero se crea una función que cuente el número de k-grama
que ocurren a lo largo de la secuencia y se agrupan según el k-grama que le
corresponde.
Por ejemplo para una secuencia binaria aleatoria verdadera
con una longitud k=1, 000,000 se tiene:
Posteriormente se obtiene la probabilidad de ocurrencia de
cada k-grama, utilizando la siguiente secuencia:
Para los monogramas
se tiene:
En donde P1 es la probabilidad de ocurrencia de los unos,
K=1, 000,000 es la longitud de la secuencia de 0 y 1 analizada, N1=500, 000 es
el número de unos que aparece en toda la secuencia, 0.5 es la probabilidad
ideal con la cual debe aparecer el 1.
P0 es la probabilidad de ocurrencia de los 0, K=1000000 es
la longitud de la secuencia de 0 y 1 analizada, N0=500, 000 es el número de 0
que aparece en toda la secuencia, 0.5 es la probabilidad ideal con la cual debe
aparecer el 0, Pt e la suma de las probabilidades de ocurrencia de 1 y 0, y debe ser igual a uno.
De esta forma, se comprueba que el número de unos tiene que
ser aproximadamente igual número de 0 y que la probabilidad de ocurrencia de todas las palabras de
longitud una a lo largo de toda la secuencia tienen la misma probabilidad de
ocurrencia, por lo cual la existencia de esta palabra es aleatoria.
Este mismo análisis se lleva a cabo para las siguientes
gramas.
Para los di-gramas se
tiene:
En donde P00 es la probabilidad de ocurrencia del grama o
combinación 00, K=1, 000,000 es la longitud de la secuencia de 0 y 1 analizada, N00=25000 es el número de
veces que aparece a lo largo de la secuencia el grama 00, 0.25 es la
probabilidad ideal con la cual debe aparecer el grama de la longitud 2.
De la misma manera ocurre para las demás palabras 01, 10,
11, y finalmente Pt es la suma de todas las probabilidades, la cual debe ser
igual a uno. De esta forma, se comprueba que la ocurrencia de todas las
palabras de longitud 2 a lo largo de toda la secuencia tiene la misma
probabilidad de ocurrencia, por lo cual la existencia de esta palabra es
aleatoria.
Este mismo análisis se lleva a cabo para las siguientes
gramas:
Para los tri-gramas
se tiene:
Para los cuatro-grama
se tiene:
Para los cinco-grama
se tiene:
Para los hexa-gramas se tienen 2^6=64 combinaciones de 0 y 1
con una probabilidad de ocurrencia para cada combinación de p= 0.01562 y para
los hepta-gramas se tienen 2^7=128 combinaciones de 0 y 1 con una probabilidad
de ocurrencia de cada combinación de p= 0.00781.
Para el análisis que se describe en este trabajo consideramos
que basta con analizar hasta hepta-gramas, debido a los bueno resultados que
podemos obtener con estas 128 combinaciones a lo largo de la secuencia dada,
además que la aparición de combinaciones de más de 8 dígitos es muy baja y se
puede despreciar.
En la siguiente tabla se observa mejor la probabilidad que
le corresponde a cada grama según la probabilidad de ocurrencia relativa para
cada combinación de 0 y 1:
INTERPRETACIÓN DEL POSTULADO DE GOLOMB G3
La auto correlación AC(K) fuera de fase es constante por
todo valor de k. La función de auto correlación AC(K) de una secuencia de
periodo T se define como:
Donde C representa el número de coincidencias y D es el
número de no coincidencias entre la secuencia de T. La auto correlación está en
fase y AC(k)=1. Si T no es divisor de k,
entonces esta fuera de fase y AC(k) toma valores en el intervalo [-1.1]. La
función diferencia entre dos símbolos. Esto se realiza restando el número de
las discordancias D y el número de las concordancias C. Existe una discordancia
cuando, para una posición en las secuencias original y desplazadas los bits son
diferentes. En este caso contrario hay una concordancia.
Ejemplo:
Considere la secuencia 10 11 01, calculando las
concordancias y discordancias contra la secuencia desplazada y representando la
existencia de las concordancias con 1 y en su defecto a las discordancias con
0, se tiene los siguientes cálculos de desplazamientos:
La función de auto correlación también se puede definir por:
Para k= 0, 1, 2, 3,…, N-1
La función de auto correlación equivale a sumar todas las
concordancias y restarle todas las discordancias. Por lo que el número de concordancias esta expresado por:
El número de
discordancias esta expresado por:
Así la función de auto correlación para secuencias binarias
se expresaría como:
A continuación se muestra en la siguiente gráfica de auto
correlación normalizada, definida por Halsall.
Se observa que cuando las secuencias estás en fase k=0, hay
un valor máximo de coincidencias y conforme la secuencia se desplaza k
posiciones el valor de la auto correlación tiende a 0. Esto mide la cantidad de
similitud entre la secuencia original y la secuencia desplazada en cada
posición.
Por lo tanto, el postulado 3 de Golomb plantea que la
función se auto correlación de una secuencia pseudoaleatoria es máxima en un
desplazamiento 0 y decrece a un nivel plano para los demás desplazamientos, por lo que el espectro se
comporta como una delta. Puesto que una delta es una constante al calcular su
transforma de Fourier, el espectro esperado será una componente de energía en
cada frecuencia, es decir se obtiene un espectro muy semejante al del ruido
blanco, cunado la longitud n de la secuencia sea muy grande.












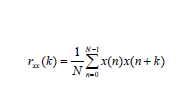




No hay comentarios.:
Publicar un comentario